[c言語]隣接リストで深さ優先探索を実装

隣接リスト

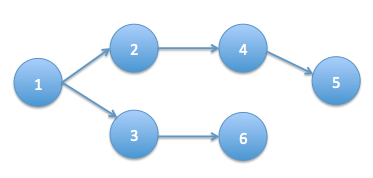
今回は、上記の経路(有向グラフ)を、隣接リストで表現します。

#define ROW 6
#define COL 3

int pathList[ROW][COL] = {
	{0},
	{2, 3, 0},
	{4, 0},
	{6, 0},
	{5, 0},
	{0}
};

深さ優先探索

深さ優先探索は、行き止まりに到達するまで、先に先に経路を進めるイメージです。
再起を使うとシンプルに書けてしまいます。

dfs()の引数で、スタート地点とゴール地点を設定します。
通過した地点は、配列route[地点]の要素に1を代入します。
ゴール地点まで到達したら、Found targetと表示します。
あとは、次の地点の経路をdfs()の引数に設定して、dfs()自身を再帰呼び出しします。

void dfs(int start, int target){
	int i;
	
	route[start] = 1;
	printf("%d→", start);
	if(start == target){
		printf("Found target");
		return;
	}
	for(i = 0; pathList[start][i] != 0; i++){
		if(route[pathList[start][i]] == 0){
			dfs(pathList[start][i], target);
		}
	}
}

サンプルコード

下記がサンプルコードになります。

 $ cat sample.c 
#include 
#define ROW 6
#define COL 3

int pathList[ROW][COL] = {
	{0},
	{2, 3, 0},
	{4, 0},
	{6, 0},
	{5, 0},
	{0}
};

int route[ROW];

void initRoute(){
	int i;
	for(i = 0; i < ROW; i++){
		route[i] = 0;
	}
	
	return;
}

void dfs(int start, int target){
	int i;
	
	route[start] = 1;
	printf("%d→", start);
	if(start == target){
		printf("Found target");
		return;
	}
	for(i = 0; pathList[start][i] != 0; i++){
		if(route[pathList[start][i]] == 0){
			dfs(pathList[start][i], target);
		}
	}
}

int main(){
	initRoute();
	dfs(1, 6);
		
	return 0;
}

 $ gcc -o sample sample.c
 $ ./sample 
1→2→4→5→3→6→Found target